Hello! I’ve been thinking about writing a zine about how things are represented on computers in bytes, so I was thinking about floating point.
I’ve heard a million times about the dangers of floating point arithmetic, like:
- addition isn’t associative (
x + (y + z)is different from(x + y) + z) - if you add very big values to very small values, you can get inaccurate results (the small numbers get lost!)
- you can’t represent very large integers as floating numbers
- NaN/infinity values can propagate and cause chaos
- there are two zeros (+0 and -0), and they’re not represented the same way
- denormal/subnormal values are weird
But I find all of this a little abstract on its own, and I really wanted some
specific examples of floating point bugs in real-world programs.
So I asked on Mastodon for
examples of how floating point has gone wrong for them in real programs, and as
always folks delivered! Here are a bunch of examples. I’ve also written some
example programs for some of them to see exactly what happens. Here’s a table of contents:
how does floating point work?
floating point isn’t “bad” or random
example 1: the odometer that stopped
example 2: tweet IDs in Javascript
example 3: a variance calculation gone wrong
example 4: different languages sometimes do the same floating point calculation differently
example 5: the deep space kraken
example 6: the inaccurate timestamp
example 7: splitting a page into columns
example 8: collision checking
None of these 8 examples talk about NaNs or +0/-0 or infinity values or
subnormals, but it’s not because those things don’t cause problems – it’s just
that I got tired of writing at some point :).
Also I’ve probably made some mistakes in this post.
how does floating point work?
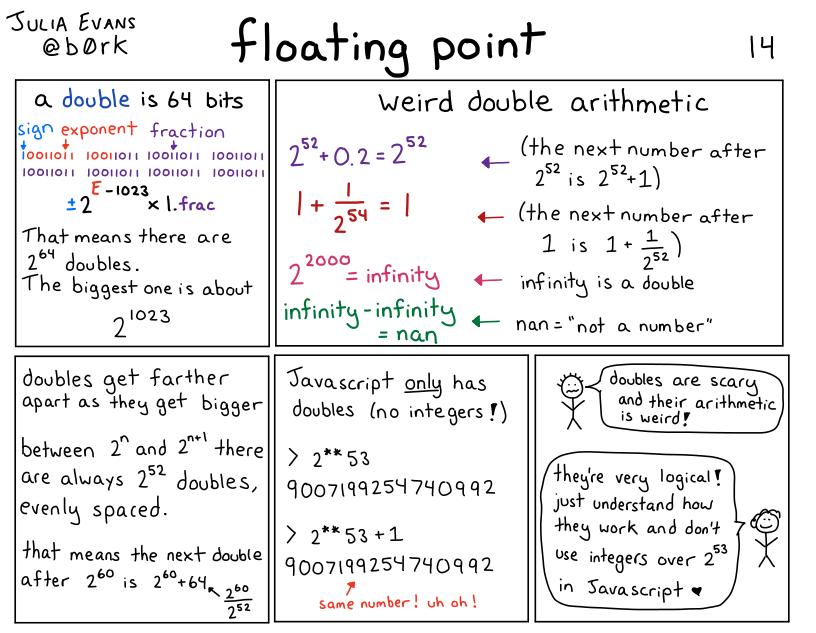
I’m not going to write a long explanation of how floating point works in this post, but here’s a comic I wrote a few years ago that talks about the basics:
floating point isn’t “bad” or random
I don’t want you to read this post and conclude that floating point is bad.
It’s an amazing tool for doing numerical calculations. So many smart people
have done so much work to make numerical calculations on computers efficient and
accurate! Two points about how all of this isn’t floating point’s fault:
- Doing numerical computations on a computer inherently involves
some approximation and rounding, especially if you want to do it
efficiently. You can’t always store an arbitrary amount of precision for
every single number you’re working with. - Floating point is standardized (IEEE 754), so operations like addition on
floating point numbers are deterministic – my understanding is that 0.1 +
0.2 will always give you the exact same result (0.30000000000000004), even
across different architectures. It might not be the result you expected,
but it’s actually very predictable.
My goal for this post is just to explain what kind of problems can come up with
floating point numbers and why they happen so that you know when to be
careful with them.
Now let’s get into the examples.
example 1: the odometer that stopped
One person said that they were working on an odometer that was continuously
adding small amounts to a 32-bit float to measure distance travelled, and
things went very wrong.
To make this concrete, let’s say that we’re adding numbers to the odometer 1cm
at a time. What does it look like after 10,000 kilometers?
Here’s a C program that simulates that:
#include
int main() {
float meters = 0;
int iterations = 100000000;
for (int i = 0; i < iterations; i++) {
meters += 0.01;
}
printf("Expected: %f kmn", 0.01 * iterations / 1000 );
printf("Got: %f km n", meters / 1000);
}
and here’s the output:
Expected: 10000.000000 km
Got: 262.144012 km
This is VERY bad – it’s not a small error, 262km is a LOT less than 10,000km. What went wrong?
what went wrong: gaps between floating point numbers get big
The problem in this case is that, for 32-bit floats, 262144.0 + 0.01 = 262144.0.
So it’s not just that the number is inaccurate, it’ll actually never increase
at all! If we travelled another 10,000 kilometers, the odometer would still be
stuck at 262144 meters (aka 262.144km).
Why is this happening? Well, floating point numbers get farther apart as they get bigger. In this example, for 32-bit floats, here are 3 consecutive floating point numbers:
- 262144.0
- 262144.03125
- 262144.0625
I got those numbers by going to https://float.exposed/0x48800000 and incrementing the ‘significand’ number a couple of times.
So, there are no 32-bit floating point numbers between 262144.0 and 262144.03125. Why is that a problem?
The problem is that 262144.03125 is about 262144.0 + 0.03. So when we try to
add 0.01 to 262144.0, it doesn’t make sense to round up to the next number. So
the sum just stays at 262144.0.
Also, it’s not a coincidence that 262144 is a power of 2 (it’s 2^18). The gaps
been floating point numbers change after every power of 2, and at 2^18 the gap
between 32-bit floats is 0.03125, increasing from 0.016ish.
one way to solve this: use a double
Using a 64-bit float fixes this – if we replace float with double in the above C program, everything works a lot better. Here’s the output:
Expected: 10000.000000 km
Got: 9999.999825 km
There are still some small inaccuracies here – we’re off about 17 centimeters.
Whether this matters or not depends on the context: being slightly off could very
well be disastrous if we were doing a precision space maneuver or something, but
it’s probably fine for an odometer.
Another way to improve this would be to increment the odometer in bigger chunks
– instead of adding 1cm at a time, maybe we could update it less frequently,
like every 50cm.
If we use a double and increment by 50cm instead of 1cm, we get the exact
correct answer:
Expected: 10000.000000 km
Got: 10000.000000 km
A third way to solve this could be to use an integer: maybe we decide that
the smallest unit we care about is 0.1mm, and then measure everything as
integer multiples of 0.1mm. I have never built an odometer so I can’t say what
the best approach is.
example 2: tweet IDs in Javascript
Javascript only has floating point numbers – it doesn’t have an integer type.
The biggest integer you can represent in a 64-bit floating point number is
2^53.
But tweet IDs are big numbers, bigger than 2^53. The Twitter API now returns
them as both integers and strings, so that in Javascript you can just use the
string ID (like “1612850010110005250”), but if you tried to use the integer
version in JS, things would go very wrong.
You can check this yourself by taking a tweet ID and putting it in the
Javascript console, like this:
>> 1612850010110005250
1612850010110005200
Notice that 1612850010110005200 is NOT the same number as 1612850010110005250!! It’s 50 less!
This particular issue doesn’t happen in Python (or any other language that I
know of), because Python has integers. Here’s what happens if we enter the same number in a Python REPL:
In [3]: 1612850010110005250
Out[3]: 1612850010110005250
Same number, as you’d expect.
example 2.1: the corrupted JSON data
This is a small variant of the “tweet IDs in Javascript” issue, but even if
you’re not actually writing Javascript code, numbers in JSON are still sometimes
treated as if they’re floats. This mostly makes sense to me because JSON has
“Javascript” in the name, so it seems reasonable to decode the values the way
Javascript would.
For example, if we pass some JSON through jq, we see the exact same issue:
the number 1612850010110005250 gets changed into 1612850010110005200.
$ echo '{"id": 1612850010110005250}' | jq '.'
{
"id": 1612850010110005200
}
But it’s not consistent across all JSON libraries Python’s json module will decode 1612850010110005250 as the correct integer.
Several people mentioned issues with sending floats in JSON, whether either
they were trying to send a large integer (like a pointer address) in JSON and
it got corrupted, or sending smaller floating point values back and forth
repeatedly and the value slowly diverging over time.
example 3: a variance calculation gone wrong
Let’s say you’re doing some statistics, and you want to calculate the variance
of many numbers. Maybe more numbers than you can easily fit in memory, so you
want to do it in a single pass.
There’s a simple (but bad!!!) algorithm you can use to calculate the variance in a single pass,
from this blog post. Here’s some Python code:
def calculate_bad_variance(nums):
sum_of_squares = 0
sum_of_nums = 0
N = len(nums)
for num in nums:
sum_of_squares += num**2
sum_of_nums += num
mean = sum_of_nums / N
variance = (sum_of_squares - N * mean**2) / N
print(f"Real variance: {np.var(nums)}")
print(f"Bad variance: {variance}")
First, let’s use this bad algorithm to calculate the variance of 5 small numbers. Everything looks pretty good:
In [2]: calculate_bad_variance([2, 7, 3, 12, 9])
Real variance: 13.84
Bad variance: 13.840000000000003 <- pretty close!
Now, let’s try it the same 100,000 large numbers that are very close together (distributed between 100000000 and 100000000.06)
In [7]: calculate_bad_variance(np.random.uniform(100000000, 100000000.06, 100000))
Real variance: 0.00029959105209321173
Bad variance: -138.93632 <- OH NO
This is extremely bad: not only is the bad variance way off, it’s NEGATIVE! (the variance is never supposed to be negative, it’s always zero or more)
what went wrong: catastrophic cancellation
What’s going here is similar to our odometer number problem: the
sum_of_squares number gets extremely big (about 10^21 or 2^69), and at that point, the
gap between consecutive floating point numbers is also very big – it’s 2**46.
So we just lose all precision in our calculations.
The term for this problem is “catastrophic cancellation” – we’re subtracting
two very large floating point numbers that are very close together, and that
just isn’t going to give you the right answer.
The blog post I mentioned before
talks about the a better algorithm people use to compute variance called
Welford’s algorithm, which doesn’t have the catastrophic cancellation issue.
And of course, the solution for most people is to just use a scientific
computing library like Numpy to calculate variance instead of trying to do it
yourself 🙂
example 4: different languages sometimes do the same floating point calculation differently
A bunch of people mentioned that different platforms will do the same
calculation in different ways. One way this shows up in practice is – maybe
you have some frontend code and some backend code that do the exact same
floating point calculation. But it’s done slightly differently in Javascript
and in PHP, so you users end up seeing discrepencies and getting confused.
In principle you might think that different implementations should work the
same way because of the IEEE 754 standard for floating point, but here are a
couple of caveats that were mentioned:
- math operations in libc (like sin/log) behave differently in different
implementations. So code using glibc could give you different results than
code using musl - some x86 instructions can use 80 bit precision for some double operations
internally instead of 64 bit precision. Here’s a GitHub issue talking about
that
I’m not very sure about these points and I don’t have concrete examples I can reproduce.
example 5: the deep space kraken
Kerbal Space Program is a space simulation game, and it used to have a bug
called the Deep Space Kraken where when
you moved very fast, your ship would start getting destroyed due to floating point issues. This is similar to the other problems we’ve talked out involving big floating numbers (like the variance problem), but I wanted to mention it because:
- it has a funny name
- it seems like a very common bug in video games / astrophysics / simulations in general – if you have points that are very far from the origin, your math gets messed up
Another example of this is the Far Lands in Minecraft.
example 6: the inaccurate timestamp
I promise this is the last example of “very large floating numbers can ruin your day”.
But! Just one more! Let’s imagine that we try to represent the current Unix epoch in nanoseconds
(about 1673580409000000000) as a 64-bit floating point number.
This is no good! 1673580409000000000 is about 2^60 (crucially, bigger than 2^53), and the next 64-bit float after it is 1673580409000000256.
So this would be a great way to end up with inaccuracies in your time math. Of
course, time libraries actually represent times as integers, so this isn’t
usually a problem. (there’s always still the year 2038 problem, but that’s not
related to floats)
In general, the lesson here is that it’s better to use integers if you can.
example 7: splitting a page into columns
Now that we’ve talked about problems with big floating point numbers, let’s do
a problem with small floating point numbers.
Let’s say you have a page width, and a column width, and you want to figure out:
- how many columns fit on the page
- how much space is left over
You might reasonably try floor(page_width / column_width) for the first
question and page_width % column_width for the second question. Because
that would work just fine with integers!
In [5]: math.floor(13.716 / 4.572)
Out[5]: 3
In [6]: 13.716 % 4.572
Out[6]: 4.571999999999999
This is wrong! The amount of space left is 0!
A better way to calculate the amount of space left might have been
13.716 - 3 * 4.572, which gives us a very small negative number.
I think the lesson here is to never calculate the same thing in 2 different ways with floats.
This is a very basic example but I can kind of see how this would create all
kinds of problems if I was doing page layout with floating point numbers, or
doing CAD drawings.
example 8: collision checking
Here’s a very silly Python program, that starts a variable at 1000 and
decrements it until it collides with 0. You can imagine that this is part of a
pong game or something, adn that a is a ball that’s supposed to collide with
a wall.
a = 1000
while a != 0:
a -= 0.001
You might expect this program to terminate. But it doesn’t! a is never 0,
instead it goes from 1.673494676862619e-08 to -0.0009999832650532314.
The lesson here is that instead of checking for float equality, usually you
want to check if two numbers are different by some very small amount. Or here
we could just write while a > 0.
that’s all for now
I didn’t even get to NaNs (the are so many of them!) or infinity or +0 / -0 or subnormals, but we’ve
already written 2000 words and I’m going to just publish this.
I might write another followup post later – that Mastodon thread has literally
15,000 words of floating point problems in it, there’s a lot of material! Or I
might not, who knows 🙂










Superb, congratulations